Is that a typo or did a 13 year old Dan Warren really do a 1K in 2:57.0 ?mikvan52 wrote:
If it's a typo; it's C2'spmacaula wrote:Is that a typo or did a 13 year old Dan Warren really do a 1K in 2:57.0 ?mikvan52 wrote:
If so, gotta believe he was recruited directly to the national team of whatever country he is from & will not be a Ltwt by the time he is done growing !
Cheers. Patrick.
Could be a misconfigured PM3/PM4 on his ergo.mikvan52 wrote:
If it's a typo; it's C2's
If it's not for real..... (hmmm)
[snip]
..or, maybe "Dan Warren" is, in fact, a 13 yr-old pit bull terrier and they tied some meat to the erg handle
Thank you for taking this interest in the perathlon. Actually the 2k is the only distance that has the 100 percent WR curve. Any new 2k records that are above 100 percent of the curve, result in an adjustment of the curve. I've not yet included updated WR's, notably Stepansen's 5:58.5, since September 08, 2008, though this would be relatively easy to do. Again, however, this would be only for the 2k. Also note my comment at the bottom of this post, that I did not say much about in the forum at the time, whereby the Perathlon revision could result in significantly higher scores for events on either side of the 2k. This is because the other 9 events are based on the previous year's rankings, rather than the fastest possible time for each of the other 9 events.NavigationHazard wrote:if the 2k WRs represent the best possible performances on an erg, all Perathlon scores by all rowers at all other distances should be less than 1000 points.
I checked that and got 104.x points.J. Ortega's 2:39.6 1k at age 25 yields 1017.6 Perathlon points.
Yes, because that time is not as close to the WR curve as some other 50+ performances.Andy Ripley's 50+ MHW record of 6:07.7 -- which has stood since 1998 -- yields but 969.2 Perathlon points.
Because only the 2k is the most popular, most competitive event, and has the highest quality times and WRs.If nothing else, why not calculate everything in relation to the 1k records, since Ortega's performance offhand looks like the single best result ever accepted as a record.
Age>500 m> 1000m> 2000m
30 > 1:24.5 > 2:57.8 > 6:06.4
40 > 1:24.7 > 3:01.0 > 6:18.2
50 > 1:24.2 > 3:03.3 > 6:25.1
60 > 1:29.9 > 3:16.7 > 6:42.5
70 > 1:38.4 > 3:29.1 > 7:13.4
80 > 1:41.1 > 3:47.2 > 7:42.0
and here is the (rough) calculated fall within each distance:
Age>500 m> 1000m>2000m
30 > 100% > 100% > 100%
40 > 100% > 98% > 97%
50 > 100% > 97% > 95%
60 > 96% > 89% > 90%
70 > 83% > 82% > 82%
80 > 80% > 72% > 73%
From the second table we can surmise the following averages drops:
Age>500 m> 1000m>2000m
30 > ...
40 > (avg = 98%) IOW: 2% less than the 30 yr age group
50 > (avg = 97%) IOW: 3% less
60 > (avg = 92%) IOW: 8% less
70 > (avg = 82%) IOW: 18% less
80 > (avg = 75%) IOW: 25% less
Probably right on the curve would be the best prediction. For example, the record by Ripley could be improved by a new record on the curve.mikvan52 wrote:I am interested, rather, in how far off a curve generated by considering all WR performances one could expect a new world record to occur.
In the case of Ripley's record, it would be about 3% faster.Is it statistically acceptable to expect a bone fide result at 500m, 1k, or 2k that deviates from such an age vs performance to be 1% ? 2%? faster??
Nosmo created a similar curve from the Perathlon a few years ago. It is still on the site but doesn't show up due some changing around of the format.Here, for lack of a better graphic model, is a curve: Imagine that is was created using the column in bold of 2000m WR from the top of this post.
http://www.moshplant.com/direct-or/bezier/curve01.gif
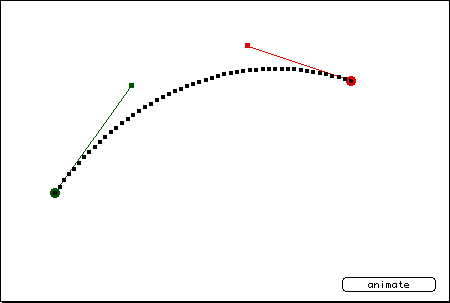
Below the curve would be anyone slower than the record.Now, what interests me is the cluster of future performances that would populate the white space below and above the curve.
Not very much, no. Historically it has not been very much.The deviation percentage couldn't be very much, could it?
Things you also see is this, above 30 you don,t see many former top otw rowers in teh rankings. They have done there hard work and don,t continue to do this while they start aging and loose some performance. Lot's stop completely, others keep training but don,t push themselves, they just keep fit. You don,t see them in rankings, sometime they pop up years later.bloomp wrote:So as a 'group' of ergers ages, the percentage by which they beat a WR will continually decrease?
Here's what I'm seeing. Barring a newcomer to a group of people aging across that 10-year span, you will have a very fixed percentage as to how much that group will break the previous groups WR as they approach a specific age. For example, as the people who are in the 30-39 group become 40-49, they will break the WR 2k times by a percentage less than the 20-29 year old rowers who will be 30-39 soon.
Bah forgot to add this: A newcomer completely skews the data because they do not have results from a previous 'group'. With the younger ages (12-18) it makes sense that they wouldn't have data points to compare, but by the time someone is 29, they've probably posted 2k scores for the last 5, probably 10 years. What you could also expect to see is IF a new rower set an age group WR, there would be less of a percentage difference between their WR and the one that beats it.
On a similar note, and I am not sure if this is what you were exactly getting at, there will always be a faster time so there must always be an expectation that the current records will fade. I think we can attribute that to something very positive, the fact that the rowing community has been able to incorporate a rewarding training method at an earlier and earlier age. It doesn't cause athletes to burn out, and hopefully they will continue rowing (and breaking progressive WRs) into their old age.
You bring up some excellent points, my friend.hjs wrote:the people who are on top for a while also stop ranking pieces when they can,t pb anymore.
...you often see here newcomers, coming from an other sport of completely new, If those people are relative talented on the erg and see themselves high in the rankings they often train hard for a while and reach there current max more or less, but after a few years their age is creeping up on them and there performance starts dropping....
At this point most of them also drop out, or stop ranking their rows. I could name many examples from my head but I won,t start naming names.
In short, it's very difficult for people to keep motivated while they start getting less good. We need hard work to be rewarded and if it's not we stop. Makes sense.
-- Seiler et al., Gender Differences In Rowing Performance And Power With Aging, Medicine & Sport Science 30 121-7 Ja '98.Conversion of ergometer time to average applied power reveals that average power for the best male and female rowers declines linearly at the same absolute rate of 4 W*yr[sup-1]. The incongruence between the age-power and age-performance time relationships is a mechanical issue, not a physiological one. The relationship between a change in muscular power output and the corresponding change in movement velocity of an object moving through air or water is not linear because of the exponential relationship between movement velocity and the resulting drag force acting on the object (10,11). Power is a third-order polynomial function of velocity whether one is moving through air or water. This relationship is also true for the rowing ergometer used in this study because the resistance is created by a circular wind vane moving through air. Interpretation of performance data from events such as time-trial cycling, flat-water kayaking, on-water and ergometer rowing, and swimming is complicated by this nonlinearity between applied power and velocity. In all of these events, body weight is supported, and air and/or water drag is the primary resistance to movement. In contrast, the impact of wind drag on running is relatively less important compared with the resistance caused by gravity at typical running velocities in endurance events (16-24 km*h[sup-1]).
Gender differences in the pattern of performance decline are also created by the different peak average powers produced by elite men and women. Young men produce higher power outputs than women, but lose power at a similar absolute rate (4 W*yr[sup-1]). Thus, their relative performance power is better maintained (Fig. 5b). Cross-sectionally, the relative power decline in elite men is 0.9% per year versus 1.2% per year in elite women. At young ages where the gender performance difference is most dramatic, the mean external power output sustained by elite men is nearly 50% higher than same-age elite women. Young elite men average 460 W compared to 325 W for their female counterparts. These power values are almost identical to the average power outputs of the 1992 male and female Olympic rowing teams in a 2000-m race simulation (instead of the 2500-m distance used in the present data) on the CII ergometer (467 W, N = 35 men and 310 W, N = 25 women, (4)). The 50% gender difference in ergometer power output in these national team members was paralleled by a 45% difference in absolute VO[sub2max] (6.25 L*min[sup-1] vs 4.37 L*min[sup-1], (4)). This substantial gender difference in external power output is associated with only a 15% greater mean velocity on the ergometer and an 8-10% greater velocity in the boat (where increased body weight in men results in increased boat wetted surface area and attenuates the benefit of increased power). At high ergometer (or boat) velocities, large changes in mechanical power applied to the oar will elicit smaller absolute changes in velocity compared with the same power increment applied at low velocities. Consequently, although mean power declines in parallel in men and women between the mid-20s and mid-50s (Fig. 4b), the impact on rowing ergometer velocity is less substantial in elite young to middle-aged men because they perform on a steeper portion of the exponential power-velocity curve. After this age, men perform on a shallower portion of this curve and performance times decrease more for the same decrement in power. On the basis of the power-velocity relationship, the conversion of performance time to mean power yields a more meaningful quantification of physiological decline across age. This conversion can be made accurately on rowing ergometer performance, but it has relevance to the interpretation of performance data from several other sports where such a conversion is more problematic.
